Prompt:
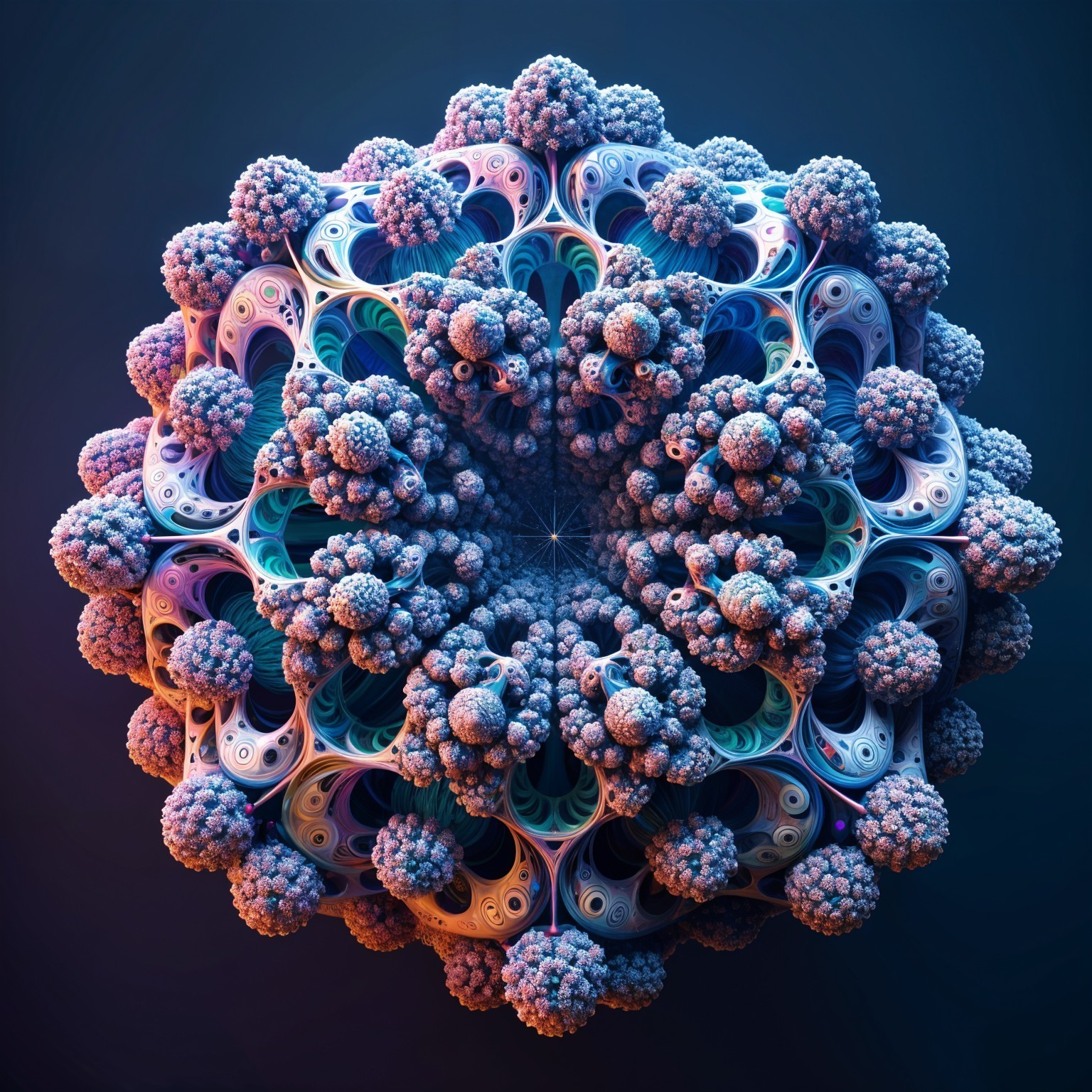
A manifold exhibiting emergent topological extravaganza, using exact mathematical iteration: for points \mathbf{c} = (c_x, c_y, c_z) \in \mathbb{R}^3, iterate \mathbf{z}_{k+1} = f_8(\mathbf{z}_k) + \mathbf{c}
from \mathbf{z}_0 = (0,0,0), where f_8(\mathbf{z}) is 12.7887th-power in spherical coordinates: let \varphi = \frac{\sqrt(5)+1)}{2}; convert \mathbf{z} = (x,y,z)
to r = \sqrt{x^{\left\{\frac{\pi}{\varphi}\right\}}+y^{\left\{\frac{\pi}{\varphi}\right\}}+z^{\left\{\frac{\pi}{\varphi}\right\}}}
,\theta = \atan2(y,x) \in [0,2\pi), \phi = \arccos(z/r) \in [0,\pi]; then r' = r^12.7887,\theta' = 12.7887\theta,\phi' = 12.7887\phi; reconvert to Cartesian \mathbf{z}' = r' (\sin\(\sin\phi'\)\cdot\cos\(\cos\theta'\), \sin\(\sin\phi'\)\cdot\sin\(\sin\theta'\), \cos\(\cos\phi'\) ). Bailout at r_k > 248.78; render the bounded set's isosurface at density threshold yielding fractal dimension D \approx 2 + \frac{\ln(12.7887)}{\ln(1/0.5)} with infinite genus g \to \infty from iterated hyperbolic saddles with PHIB = (\sqrt{5.0} \cdot 0.5 + 0.5) and Jacobian eigenvalues |\lambda_i| \approx 12.7887 r^11.7887 e^{i11.7887\arg(\mathbf{z})}, saddles where \det Jacobian > pi\cdot\PHIB. Center on \mathbf{c} \approx (0,0,-0.7)
for cardioid region, emphasizing bilateral symmetry (z-axis invariance enforcing yz-mirror), genus-7.4554 bulbs at \phi \approx \pi/2 \pm \epsilon from 12.7887-fold rotational folding (even-pair selection), central z-axis protrusion (minimal \phi-folding, radial ballooning r' = r^12.7887), and vertical depressions from polar \phi -compression. Use volumetric ray-marching with distance estimator d(\mathbf{x}) = |\mathbf{x}| - \max_k r_k^{-k}; color palette: iridescent blue background (#0000FF
) grading to translucent pink-magenta gradients (#FF1493
to #8A2BE2
) on surfaces, with subtle specular highlights on bulb edges and fractal tendrils. Lighting: soft key light from +z, rim light from +x for depth; resolution 4K, aspect 16:9, no artifacts.
 Artist
Artist